中山大学陈立教授团队在中短码系列研究取得新突破
赌博软件-在线赌博app 陈立教授团队在多元循环码的迭代译码研究工作取得了重要进展,实现了一种全新的超限译码机制,尤其适用于支撑未来超高可靠低时延通信(URLLC)的中短码。团队最新研究成果以《Shift-Sum Decoding of Non-Binary Cyclic Codes》发表于信息论领域国际顶级期刊IEEE Transactions on Information Theory,论文第一作者为邢炯跃博士(中山大学电子与信息工程学院2020届博士毕业生),通信作者为陈立教授。
随着各种实时网络业务的普及,从在线教育到电子医疗、从工业自动化到无人驾驶,高效可靠的数据传输显得尤为重要。信道编码技术在其中发挥着关键作用,确保了数据高效可靠的传输,从而提供更多元、更快速和更高质的移动信息服务。“万物智联”已成为6G通信网络的技术愿景。针对URLLC业务场景,如何设计既具备强大纠错能力又可实现低时延译码的信道编码已成为学术界和工业界的聚焦点,代数编码具有优美而丰富的数学结构,可望持续提升纠错能力和译码效率,在新一代通信网络中发挥重要作用。
循环码是一类广泛应用的代数编码,常用的循环码包括BCH码和Reed-Solomon(RS)码等,它们不仅应用于无线通信系统,还在磁存储、二维码和可见光通信系统中发挥作用。对于BCH码和RS码,工业界通常采用基于校正子的Berlekamp-Massey(BM)译码算法,它可以通过移位寄存器实现,简单高效。然而,它的纠错能力受限于码的最小汉明距离的一半,其超限译码一直是编码界公认的难题。直到1999 年,Guruswami 和Sudan提出了崭新的译码思想,重新发现并利用RS码的赋值编码特性首次实现了代数超限译码。
陈立教授团队长期从事代数编译码理论与技术研究,多次在RS码和代数几何码的高性能低复杂度译码研究中取得重要突破。2018年底,博士生邢炯跃前往德国Ulm大学访问德国科学院院士、IEEE Fellow Martin Bossert教授,双方团队由此开启了针对多元循环码的全新移加译码的合作研究。通过持续探索,团队首先提出一个面向多元循环码的启发式算法,用于搜索循环不等价的最小重量对偶码字,利用它们与接收向量的循环移位操作生成可靠值矩阵,从而确定错误位置及幅值,实现纠错。根据此度量,团队进一步提出了迭代移加译码机制,其纠错能力可以超过码的最小汉明距离的一半,形成了崭新而高效的代数码超限译码。利用信道提供的软信息,团队还进一步提出了软判决迭代移加译码,提升译码性能。值得一提的是,这类基于移加运算的超限译码仅需要多项式相乘和整数(或实数)比较,无需实数域运算,便于硬件实现,是一种可支撑高可靠低功耗通信的有效译码机制。该文章首先发表在信息论领域的顶会ISIT 2020。然而,移加译码的合理性尚不具备理论解释。团队围绕该难题另辟蹊径,创造性地通过分析每个对偶码字对可靠值矩阵的贡献度,最终从概率分析的角度揭示了移加译码的超限译码性质,赌博软件相关的文章发表在ISIT 2021。随后,团队进一步发现,结合Chase译码机制,在百比特码长下多元循环码具备比LDPC码更好的纠错性能,使多元循环码的结构特性得以被重新挖掘。针对多元循环码的迭代移加译码的系统性研究成果最终发表于今年第二期的IEEE Transactions on Information Theory期刊。
图1给出了两种多元循环码 — RS码和多元BCH码在Q元对称信道(QSC)下的译码性能。基于图中显示,迭代移加译码(HISS)相比BM译码可以获得十至百倍的纠错性能提升,实现了超限译码。该研究开启了循环码超限译码的全新路径,并由于其计算操作简单,可望在将来获得更大的工业应用。
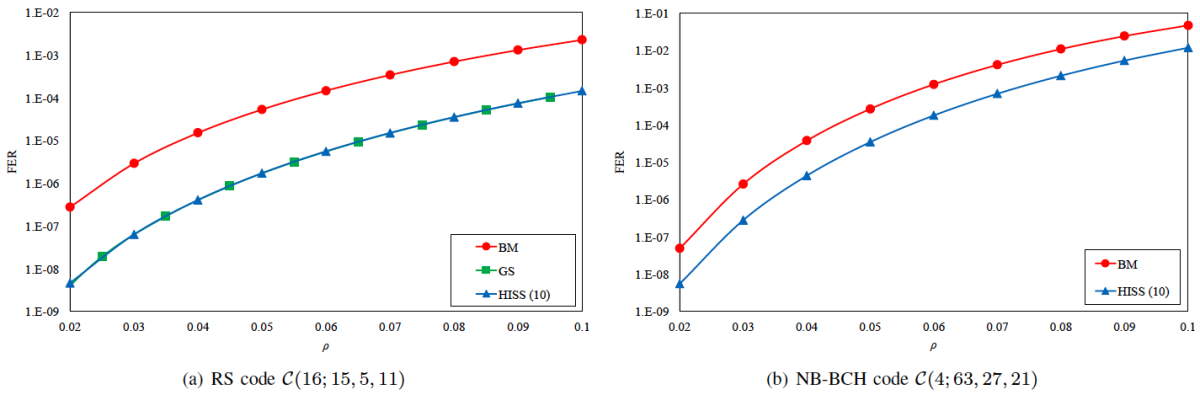
图1 RS码和多元BCH码在QSC信道下的译码性能
邢炯跃博士在读博士研究生期间,得到了国家自然科学基金和中山大学博士生访学与合作研究项目的资助,其博士论文《基于模和对偶码字的Reed-Solomon 码代数软译码》获中国电子学会信息论分会2020年度优秀博士论文奖。

2023年8月13日,邢炯跃博士返校参加“代数编译码理论与应用前沿沙龙”并做题为《Shift-Sum Decoding of Cyclic Codes》的学术报告
背景资料
IEEE Transactions on Information Theory是信息论领域国际顶级期刊,创刊于1953年,主要发表与信息传输、处理和应用相关的理论文章。
